« Robust optimal shape design strategies for systems with friction-induced instabilities and uncertain parameters »

Rendez-vous le jeudi 17 octobre 2024 à 14h00 – Amphi 203 – Bâtiment W1 de l’Ecole Centrale de Lyon à Ecully

Stratégies de conception optimale de forme robuste de structures présentant des non-linéarités de frottement et des paramètres incertains

La conception de systèmes mécaniques est un défi pour les industriels, avec des exigences croissantes en performance, en précision, et en temps de calcul.

L’optimisation de forme numérique devient de plus en plus utilisée de par son efficacité par rapport à la conception par création et modification séquentielle de la géométrie des pièces mécaniques.

Cependant, plusieurs problèmes tels que l’absence de gradient, la non-linéarité, et le coût de calcul des fonctions numériques utilisées pour quantifier la performance, constituent des difficultés majeures.

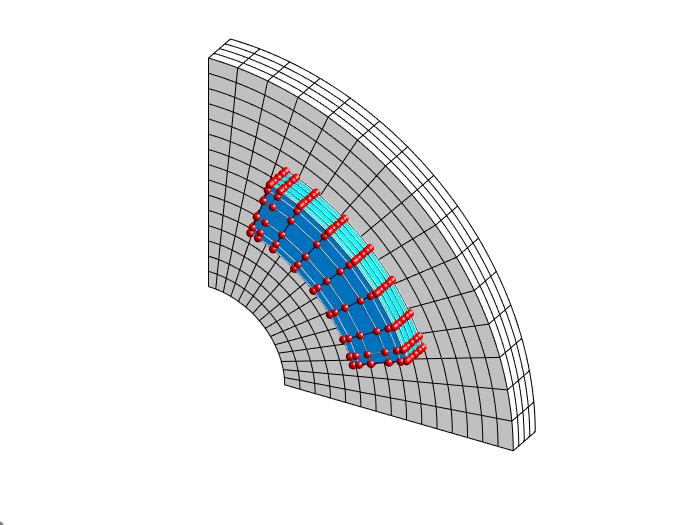
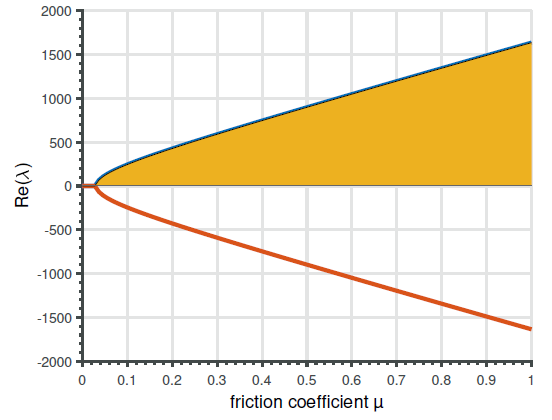
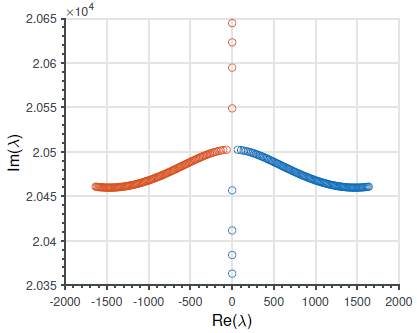
De plus, la présence d’incertitudes géométriques pouvant avoir un impact considérable sur la performance des systèmes mécaniques, celles-ci doivent être prises en compte. Les freins à disque, présents dans de nombreux types de véhicules, sont des systèmes mécaniques complexes qui ont tendance à émettre un bruit de crissement dû à un phénomène complexe d’instabilités vibratoires induites par frottement.

La quantification numérique du bruit de crissement pour sa minimisation mène à une fonction de performance sans gradient, coûteuse en temps de calcul et non-linéaire, qui représente fidèlement les principaux défis en conception optimale de systèmes mécaniques. Le travail de thèse présenté introduit de nouvelles approches pour l’optimisation robuste de forme de systèmes mécaniques, en combinant des méthodes numériques modernes, appliquées au cas d’un frein à disque sous critère de minimisation de bruit.

En se basant sur la méthode d’Analyse Isogéométrique pour la paramétrisation de la forme et l’analyse du comportement mécanique, deux approches qui permettent de rechercher des conceptions optimales équilibrant performance et robustesse aux incertitudes, sont proposées. La première approche utilise la méthode du Chaos Polynomial creux afin d’obtenir une estimation de la variabilité de la fonction de performance aux incertitudes géométriques, combinée avec un algorithme génétique pour la recherche de solutions optimales.

La capacité de cette approche à fournir des conceptions équilibrant performance et robustesse avec un coût de calcul raisonnable et une précision satisfaisante, est démontrée. La deuxième approche utilise la méthode du Krigeage bruité, méthode de méta-modélisation avec la possibilité de prendre en compte du bruit dans ses observations, pour la quantification d’incertitudes, combinée avec une stratégie d’enrichissement inspirée de l’Optimisation Bayésienne.

Les résultats obtenus démontrent le grand potentiel de cette approche à réduire le coût de calcul de l’optimisation robuste, bien que des efforts soient nécessaires pour généraliser la méthode proposée en grande dimension, ainsi que pour assurer la fiabilité de l’estimation de robustesse. Généralement, l’étude présentée illustre les difficultés associées à l’optimisation de forme robuste de systèmes mécaniques complexes, dans le cas du frein à disque sous critère de bruit, l’aspect clé étant le compromis entre coût de calcul et précision des solutions obtenues.

Les deux approches proposées constituent une contribution significative en optimisation de forme robuste et ouvrent de nouvelles perspectives dans le domaine.